Generalized Cayley-Bacharach theorem

In this post I will showcase a generalization of the famous 8 implies 9 theorem also known as Cayley-Bacharach. I will work over $\mathbb{C}$ . The exposition is due to David Eisenbud, Mark Green, and Joe Harris in the paper “CAYLEY-BACHARACH THEOREMS AND CONJECTURES” posted in BULLETIN (New Series) of the american mathematical society (Volume 33, Number 3, July 1996). The original article can be found by a google search.

Main theorem. Let $X_1,X_2\subset \mathbb{P}^2$ be plane curves of degree $d$ and $e$ , respectively, intersecting in $d\cdot e$ points $\Gamma=X_1\cap X_2=\{p_1,\hdots,p_{de}\}$ , and suppose that $\Gamma$ is the disjoint union of subsets $\Gamma'$ and $\Gamma''$ . Let $s=d+e-3$ . If $k\leq s$ is a nonnegative integer, then the dimension of the vector space of homogeneous polynomials of degree $k$ vanishing on $\Gamma'$ (modulo those containing all of $\Gamma$ ) is equal to the failure of $\Gamma''$ to impose independent conditions on homogeneous polynomials of degree $s-k$ .

Proof. See the article referenced.

Explaining the terminology. Suppose we have three distinct colinear points $\Gamma=\{p_1,p_2,p_3\}$ . Then the failure of $\Gamma$ to impose independent conditions on polynomials of degree $1$ is equal to $3-2=1$ , as a degree $1$ polynomial is a line which are determined by two points. In general, if $\Gamma\subset \mathbb{P}^2$ is a finite set of points and $\lambda\in\mathbb{N}\cup\{0\}$ is minimal such that $\lambda$ of the $\vert \Gamma\vert$ conditions suffices to imply all of them, we say that $\Gamma$ imposes $\lambda$ independent conditions on polynomials of degree $\leq m$ . The failure of $\Gamma$ to impose independent conditions of is the number $\vert\Gamma\vert-\lambda$ .

If we let $k=s$ and $\Gamma''=\{p_{de}\}$ , then we find

Corollary. Let $X_1,X_2\subset\mathbb{P}^2$ be plane curves of degree $d$ and $e$ , respectively, intersecting in $d\cdot e$ points $\Gamma=X_1\cap X_2=\{p_1,\hdots,p_{de}\}$ . If $C\subset\mathbb{P}^2$ is any plane curve of degree $s=d+e-3$ containing all but one point of $\Gamma$ , then $C$ contains all of $\Gamma$ .

Proof. Setting $k=s=d+e-3$ and $\Gamma''=\{p_{de}\}$ in the main theorem, we readily see that the dimension of homogeneous polynomials of degree $d+e-3$ vanishing on $\Gamma'=\{p_1,\hdots,p_{de-1}\}$ is equal to the failure of $\Gamma''=\{p_{de}\}$ to impose independent conditions on homogeneous polynomials of degree $0$ . The latter being equal to $0$ . Thus we conclude that there are no homogeneous polynomials of degree $d+e-3$ containing $\Gamma'$ except these containing $\Gamma$ (this is the interpretation of the “modulo those containing all of $\Gamma$ ” in the main theorem).

If we set $d=e=3$ , we recover the classical Cayley-Bacharach theorem:

Theorem (Cayley-Bacharach). Let $X_1,X_2\subset\mathbb{P}^2$ be cubic curves intersecting in $3\cdot 3=9$ points $\Gamma=X_1\cap X_2=\{p_1,\hdots,p_{9}\}$ . If $C\subset\mathbb{P}^2$ is any cubic curve containing eight of the nine points, then it also contains the last point.

“Application” Let us apply the main theorem to a problem from euclidian geometry. In the following diagram, we are asked to show that the red points lie on a circle:

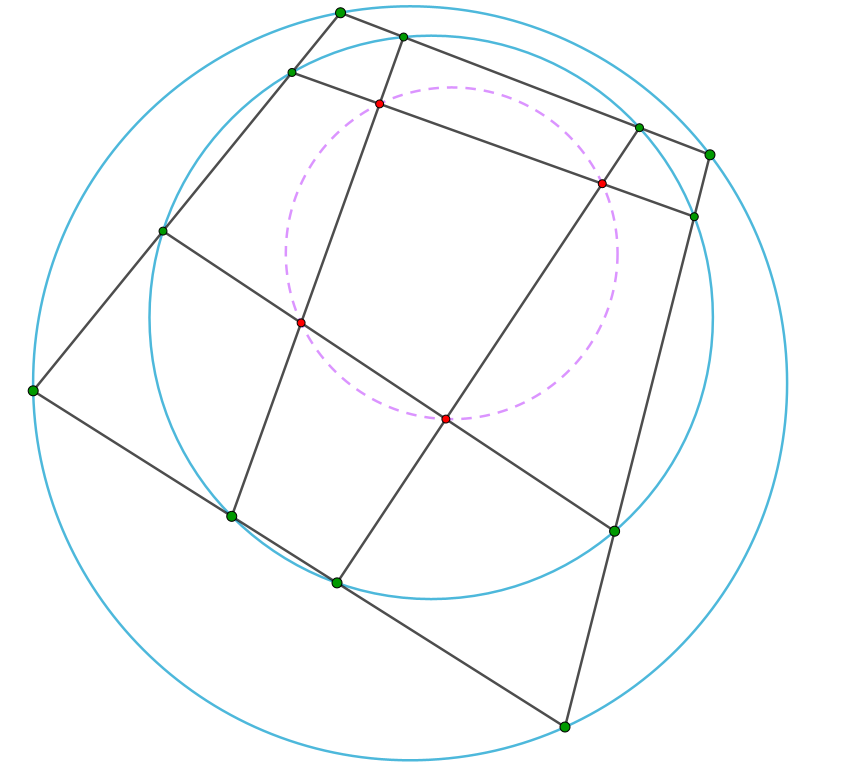
Solution. We redefine by assuming the red points lie on a circle, and then prove that the last red point lie on a line as shown in the diagram below. Let $X_1$ be the union of the three circles and $X_2$ be the union of the four green lines and the line at infinity. These curves have degree $2+2+2=6$ and $1+1+1+1+1=5$ , respectively. As the three circles all pass through the imaginary circle points at infinity, $I$ and $J$ , we must count these two points trice thrice when taking the intersection

$\begin{align*}\Gamma=X_1\cap X_2&=\{\text{The 16 real points in the picture}\}\\&\cup\{3 \text{ times }I, 3 \text{ times }J\}\\&\cup \{\text{the 4 (complex) intersections of the big circle with the two inner most green lines}\}\\&\cup\{\text{the 4 (complex) intersections of the pink circle with the two outer most green lines}\}\end{align*}$

Now, let $\Gamma'$ be the latter eight points in the intersection and $\Gamma''$ the other $22$ points. Pick $k=3\leq 8=6+5-3=s$ . Now, as there’s always a cubic passing through $8$ given points, we see that the dimension of the vector space of homogeneous polynomials of degree $k=3$ vanshing on $\Gamma'$ (modulo those containing all of $\Gamma$ ) is nonzero. Thus the failure of $\Gamma''$ to impose independent conditions on homogeneous polynomials of degree $s-k=8-3=5$ is nonzero. In particular, a degree $5$ curve passing through $21$ of the $22$ points of $\Gamma'$ must pass through the last point. So we finish by taking $C$ as the union of the four black lines and the line at infinity.

Thank you for reading.

Generalized Cayley-Bacharach theorem

1 Comment

Leave a Reply Cancel reply