IF YOU enciunbter errirs til can dinwkisd as odf
Problem 1
1. This is a local question and thus suffices to show on a cover of 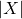 . We pick a cover making both
. We pick a cover making both 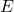 and
and 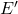 isomorphic to a direct summand of
isomorphic to a direct summand of 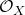 . Indeed, if we have such affine covers
. Indeed, if we have such affine covers 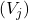 and
and  for
for 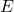 and
and 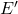 , respectively, we take the indicies s.t.
, respectively, we take the indicies s.t. 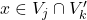 and choose some affine open
and choose some affine open 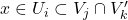 . Then clearly both
. Then clearly both 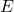 and
and 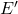 restricts to some direct summand of
restricts to some direct summand of 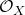 on these
on these 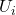 . Taking stalks, we find an exact sequence of
. Taking stalks, we find an exact sequence of 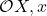 -modules:
-modules:
[
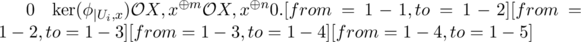
]
Using that
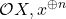
is a projective
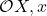
-module, we find
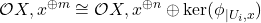
over
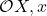
. But it is a fact that if two
-modules
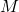
and
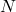
where
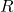
is a local ring, we have
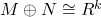
implies

and
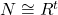
with

. Hence we find
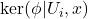
is a direct summand of
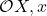
as desired. \item For a counter example, let
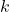
be a field and pick the ring
![Rendered by QuickLaTeX.com R=k[x]/(x^2)](https://danielphamnguyen.com/wp-content/ql-cache/quicklatex.com-bea9c5b1ed85f6ea2f107e484404f017_l3.png)
and let
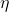
be the map of vector bundles associated to the map
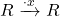
via. the
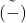
construction. As
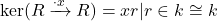
, we find that
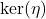
correspond tot
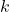
, but
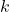
is clearly not a free
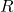
-module of finite rank. \item The assertion is false. We pick
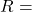
and see that the map
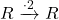
has kernel
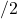
. We see that

is not a vector bundle as
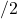
has torsion and thus isn’t flat. But then applying
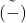
to the exact sequence
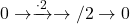
of

-modules, we get an exact sequence
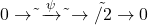
and hence conclude that
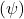
is not a vector bundle. \end{enumerate} \textbf{Problem 4.} First we note that from Problem 3 that
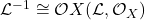
– the internal Hom sheaf. We also note that tensoring with an invertible sheaf (line bundle) preserves exactness (and thus reflects as we can tensor with the inverse line bundle), as it is locally trivial. \\
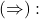
Assuming
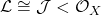
for some sheaf of ideals
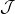
, we find an injective inclusion map
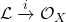
. This defines a non-zero global section of
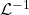
under the identification
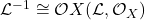
(it is non-zero as the map is injective). \\

Assume
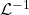
has a non-zero global section
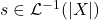
. Consider the closed subscheme
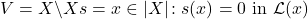
of
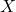
. We claim that this is a Cartier divisor whose corresponding sheaf of ideals is isomorphic to

, which finishes the problem.
\
Pick a trivializating cover
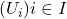
of
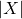
and isomorphisms
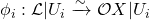
. Let
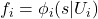
which is a non-zero-divisor, as
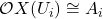
is an integral domain since
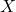
is an integral scheme. We claim that

. Indeed, when restricting to
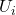
,
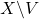
is just a standard open due to the trivialization on
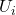
, so we see that
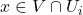
iff the corresponding prime ideal

in
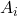
contains
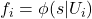
(recall
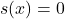
in
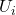
iff

). But this equivalent to
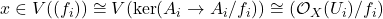
.
Recall that the corresponding sheaf of ideals is the sheaf 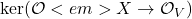 . So we want to have an exact sequence of
. So we want to have an exact sequence of 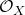 -modules
-modules
(1) 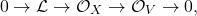
with first map is coming from tensoring the map
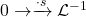
with

. It is exact at

as
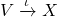
is a closed immersion and thus
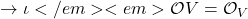
is surjective. Now, applying
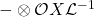
, it is equivalent to show the following is exact:
(2) 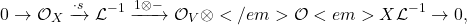
Note that the first map is injective since

is non-zero and
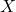
is integral (i.e. we have cancelation of non-zeros and the map is multiplication). Exactness at the middle is a local question so suffices to check on restriction to an open cover; we pick
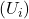
from before. Given
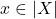
, pick open trivializing ngbh
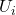
of
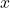
. Using that
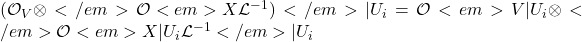
want the following to be exact:
[

]
But on stalks, this is just a consequence of exactness of the following exact sequence:
[

]
which is obviously exact.
![]() . We pick a cover making both
. We pick a cover making both ![]() and
and ![]() isomorphic to a direct summand of
isomorphic to a direct summand of ![]() . Indeed, if we have such affine covers
. Indeed, if we have such affine covers ![]() and
and ![]() for
for ![]() and
and ![]() , respectively, we take the indicies s.t.
, respectively, we take the indicies s.t. ![]() and choose some affine open
and choose some affine open ![]() . Then clearly both
. Then clearly both ![]() and
and ![]() restricts to some direct summand of
restricts to some direct summand of ![]() on these
on these ![]() . Taking stalks, we find an exact sequence of
. Taking stalks, we find an exact sequence of ![]() -modules:
-modules:![]()
![]() . So we want to have an exact sequence of
. So we want to have an exact sequence of ![]() -modules
-modules ![]()
![]()
![]()
![]()


